Calcular porcentajes: reglas, ejercicios y ejemplos de la vida cotidiana

Al igual que las fracciones, los porcentajes expresan una parte de un todo. Así, al decir que hemos recorrido un 75% del camino sabemos qué parte del camino llevamos recorrida y si es mucho o poco lo que nos queda. No te estreses: calcular porcentajes es fácil.

Reglas de cálculo o el concepto del porcentaje

El porcentaje, o tanto por ciento, puede expresar una parte de una cantidad, que puede ser mayor o menor a un todo.

De esta forma, un 50% significa la mitad de una cantidad, mientras que el 200% representará el doble de esa cantidad.

¿Y cómo se entiende el concepto? Lo veremos con un ejemplo.

En el último curso de la ESO hay un total de 100 alumnos. De entre ellos, 60 llegan al instituto en autobús o en metro. Para expresar 60 de 100 podemos utilizar la forma de 60/100 o 60%.
Un 60% de los alumnos del último curso llega al instituto en transporte público.

¿Otro ejemplo? ¡Ahí va!
Tienes una tableta de chocolate que se divide en 10 onzas. Te has comido 3 onzas. Para expresar 3 de 10 podemos utilizar la forma de 3/10 o 30%.
Te has comido un 30% de las onzas de tu tableta.

Conversión % ↔ cantidad

Vamos a asumir que 100% = 1. Siendo así, si quieres convertir el tanto por ciento a la cantidad, debes dividirlo entre 100 (dicho de otra forma: desplazar la coma dos lugares hacia la izquierda o, lo que es lo mismo, eliminarle al tanto por ciento sus dos ceros). Después solo queda quitarle el símbolo %.

Observa estos ejemplos:

1500% = 15 (1500:100 = 15)
150% = 1,5 (150:100 = 1,5)
50% = 0,5 (50:100 = 0,5)
5% = 0,05 (5:100 = 0,05)

1500% = 15
150% = 1,5
50% = 0,5
5% = 0,05

(1500:100 = 15)
(150:100 = 1,5)
(50:100 = 0,5)
(5:100 = 0,05)

¿Y para realizar la operación inversa? Si quieres convertir una cantidad en tanto por ciento, debes multiplicar el tanto por ciento por 100 (desplazar la coma dos lugares hacia la derecha o, lo que es lo mismo, “añadirle” a la cantidad dos ceros). Acuérdate de ponerle el símbolo %.

Estos son algunos ejemplos de conversión % ↔ cantidad:

0,3 = 30% (0,3•100 = 30)
30 = 3000% (30•100 = 3000)
0,45 = 45% (0,45•100 = 45)
0,024 = 2,4% (0,024•100 = 2,4)

0,3 = 30%
30 = 3000%
0,45 = 45%
0,024 = 2,4%

(0,3•100 = 30)
(30•100 = 3000)
(0,45•100 = 45)
(0,024•100 = 2,4)

MATES A GUSTO para los cursos 5° y 6°

Un método innovador de aprendizaje mediante realidad aumentada (AR).

¿Cómo calcular el tanto por ciento de una cantidad?

Para calcular el tanto por ciento de una cantidad, debes multiplicar el tanto por ciento y la cantidad. ¿Y cómo se hace eso?

Primero, cambia el tanto por ciento por una fracción simple o un decimal; solo después haz la multiplicación. Observa cómo se realiza esta operación:

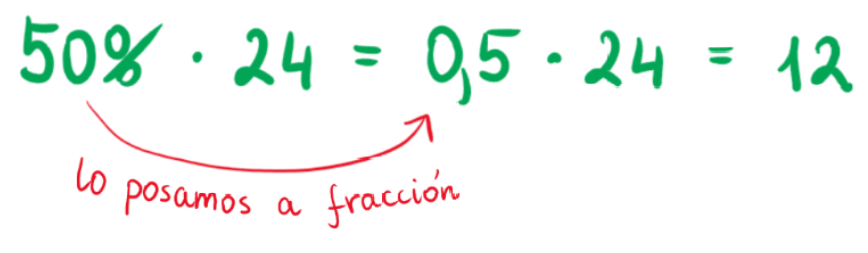
¿Cómo calcular el porcentaje que representa una cantidad en otra cantidad?

¿Necesitas calcular qué tanto por ciento de la cantidad X es la cantidad Y? ¡Eso está chupado! Lo único que tienes que hacer es expresar estas dos cantidades como una fracción y después multiplicarlas por 100%.

¿Qué tanto por ciento de 120 es 90? Vamos a ver:

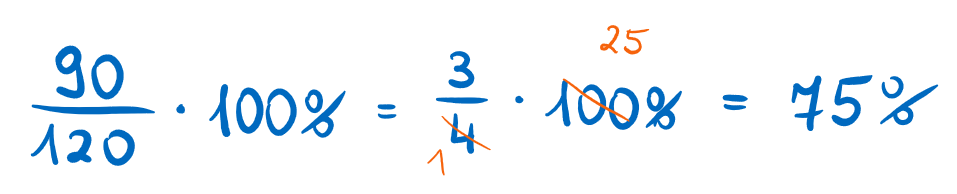
Calcular porcentajes: rebajas y subidas

Para entender los incrementos y reducciones porcentuales es bueno pensar en las subidas o rebajas en los precios de la compra (en realidad, es donde más aplicamos estos conocimientos ).

Pongamos que te quieres comprar un nuevo móvil. El modelo que te gusta cuesta 800 PLN, pero está de oferta y su precio tiene una rebaja de un 20%. ¿Cómo calcular su precio actual?

Hay dos métodos.

1. calculas el valor de la rebaja, y después se lo restas al precio inicial

2. calculas en un único paso el precio rebajado

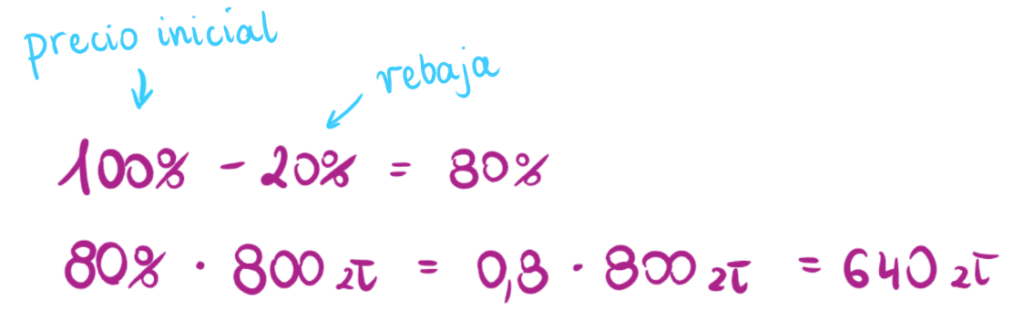
Calcular porcentajes: ejercicios

Ejercicio 1. Calcula:

¿Cuánto es el 10% de 384?
¿Cuánto es el 22% de 840?
¿Cuánto es el 310% de 24?
¿Cuánto es el 99% de 299?

Ejercicio 2. Te propones comprar una tele nueva. Antes de las Navidades, el modelo que te interesaba costaba 1400 EUR. Después de las Navidades su precio ha subido un 10%. ¿Cuánto cuesta la tele ahora?

Ejercicio 3. Estás preparando las vacaciones. El viaje que te apetece tiene un precio normal de 1300 EUR. La agencia ha aplicado un descuento “last minute” del 30%. ¿Cuánto pagarás si aprovechas la oferta?

Ejercicio 4. Un autobús realiza una ruta a la playa. La distancia entre la estación origen y la de destino es de 480 km. El autobús lleva recorridos 288 km. ¿Qué tanto por ciento de la ruta ha cubierto ya?

Ejercicio 5. Un juego de mesa costaba 20 EUR. En un primer momento su precio ha sido rebajado en un 10%, pero después ha vuelto a subir un 15%. ¿Cuál es su precio actual? ¿Cuál es la diferencia en zlotys entre el precio nuevo y el inicial?

Porcentajes en la vida cotidiana

Los porcentajes son una realidad diaria.

Nos ayudan a expresar lo que representa una parte de un todo. A sabiendas de que el todo está representado por el 100%, es fácil imaginarnos si su parte, expresada en tanto por ciento, es grande o pequeña. Justo por esto se recurre a porcentajes cuando se quieren representar resultados electorales, de la misma forma también la prensa o los medios de comunicación emplean el tanto por ciento para decirnos, por ejemplo, que el 30% de los españoles viaja en verano al extranjero.

El tanto por ciento es, además, muy cómodo a la hora de expresar diferencias, como las del precio de la gasolina en el último mes (ha subido un 10% o ha bajado un 5%). La mayoría de los comercios recurre con regularidad a las rebajas, que en ocasiones pueden ser de tipo liquidación, con descuentos de hasta un 70% en todo el género, o un discreto 20% en un producto alimentario determinado. Sea cual sea el caso, es bueno saber el ahorro que podamos hacer y comprobar si el precio expresado en el ticket coincide con lo esperado.